Pflichtteil 2016 - Aufgabe 5
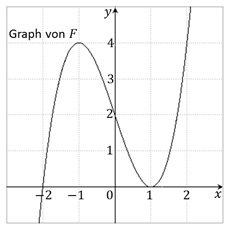
Die Abbildung zeigt den Graphen einer Stammfunktion F einer Funktion f. Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Begründen Sie jeweils Ihre Entscheidung.
(1) f(1)=F(1)
(2)
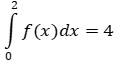
(3) f' besitzt im Bereich -1≤x≤1 eine Nullstelle.
(4) f(F(-2))>0
(5 VP)
Pflichtteil 2015 - Aufgabe 5
Die Abbildung zeigt den Graphen der Ableitungsfunktion f' einer ganzrationalen Funktion.
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.
Begründen Sie jeweils Ihre Antwort.
(1) Der Graph von f hat bei x=-3 einen Tiefpunkt.
(2) f(-2)<f(-1)
(3) f''(-2)+f'(-2)<1
(4) Der Grad der Funktion f ist mindestens 4.
(5 VP)
Pflichtteil 2014 - Aufgabe 5
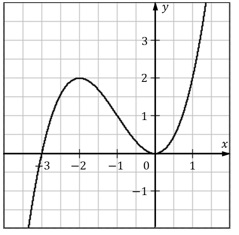
Die Abbildung zeigt die Graphen Kf und Kg zweier Funktionen f und g.
a) Bestimmen Sie f(g(3)).
Bestimmen Sie einen Wert für x so, dass f(g(x))=0 ist.
b) Die Funktion h ist gegeben durch h(x)=f(x)·g(x).
Bestimmen Sie h'(2)
(5 VP)
Pflichtteil 2013 - Aufgabe 5
Eine Funktion f hat folgende Eigenschaften:
(1) f(2)=1
(2) f'(2)=0
(3) f''(4)=0 und f'''(4)≠0
(4) Für x→+∞ und x→-∞ gilt f(x)→5
Beschreiben Sie für jede dieser vier Eigenschaften, welche Bedeutung sie für den Graphen von f hat.
Skizzieren Sie einen möglichen Verlauf des Graphen.
(5 VP)
Pflichtteil 2012 - Aufgabe 5
Eine der folgenden Abbildungen zeigt den Graphen der Funktion f mit f(x)=x3-3x-2.
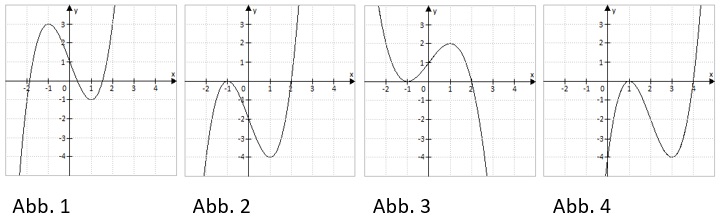
b) Von den anderen drei Abbildungen gehört eine zur Funktion g mit g(x)=f(x-a) und eine zur Funktion h mit h(x)=b·f(x).
Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie Ihre Entscheidung.
Geben Sie die Werte für a und b an.
c) Die bis jetzt nicht zugeordnet Abbildung zeigt den Graphen einer Funktion k.
Geben Sie ohne Rechnung einen Funktionsterm für k an.
(5 VP)
Pflichtteil 2011 - Aufgabe 5
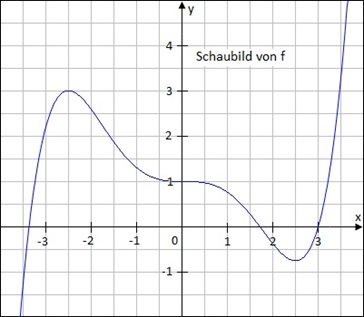
Die Abbildung zeigt das Schaubild einer Funktion f.
F ist eine Stammfunktion von f.
Begründen Sie, dass folgende Aussagen wahr sind:
(1) F ist im Bereich -3≤x≤1 monoton wachsend.
(2) f' hat im Bereich -3,5≤x≤3,5 drei Nullstellen.
(3)
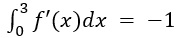
(4) O(0|0) ist Hochpunkt des Schaubilds von f'.
Pflichtteil 2010 - Aufgabe 5
Die vier Abbildungen zeigen Schaubilder von Funktionen einschließlich aller waagrechten Asymptoten.
Eines dieser Schaubilder gehört zur Funktion f mit
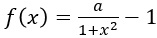 .
.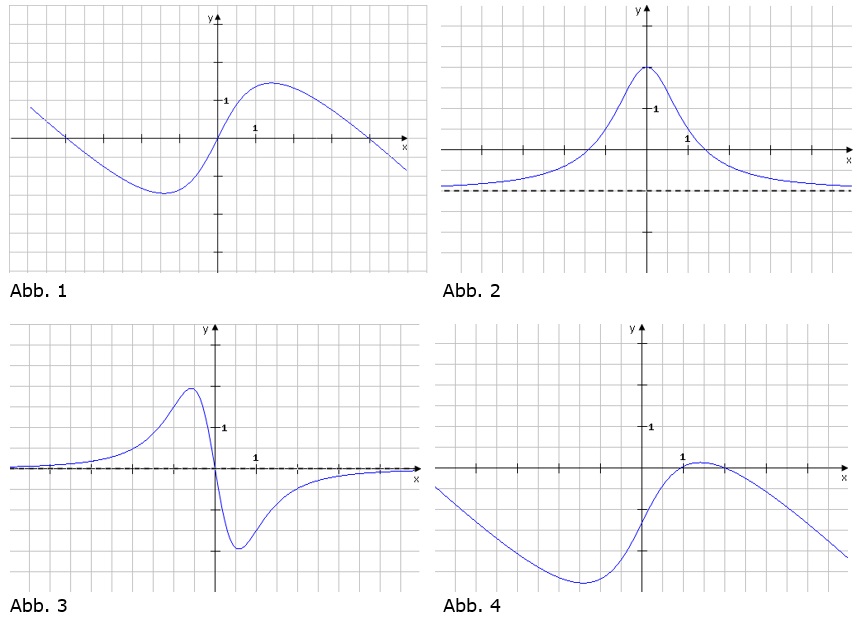
a) Begründen Sie, dass Abbildung 2 zur Funktion f gehört.
Bestimmen Sie den Wert von a.
b) Von den anderen drei Abbildungen gehört eine zur Ableitungsfunktion f' und eine zur Integralfunktion I mit
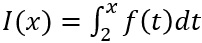 .
.Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie jeweils Ihre Entscheidung.
(5 VP)
| Downloads |
PowerPoint